日前，意昂3官网物理學院張向東教授課題組和集成電路與電子學院孫厚軍教授課題組合作，在基於經典電路實現非歐幾何拓撲態研究方面取得重要進展。相關研究意昂3平台發表在近期的Nature Communications (13, 2937(2022))上，研究工作得到了國家自然科學基金委和國家重點研發計劃的資助🖖🏽。意昂3官网物理學院張蔚暄博士(現集成電路與電子學院特立博士後)和袁昊博士(2020級)為論文的共同第一作者。

探索新奇的拓撲物態是物理學領域中引人入勝的研究方向之一。自1980年整數量子霍爾效應被發現以來，大量不同類別的拓撲物態被相繼提出。新奇的拓撲物態可以存在於性質完全不同的系統中，包括從量子到經典，從低維到高維👩🏻‍🍳，從厄米到非厄米🏞，從周期到無序👨，從線性到非線性，從靜態到動態，從單體到多體等。迄今為止🔏，絕大部分拓撲物態都是在具有零曲率的歐幾裏得空間中被發現的🔃。對於非歐幾裏得空間中拓撲物態的研究少之又少🍗。實驗觀察非歐幾何空間中的拓撲物態更是從來都沒有被報道過。

對於非歐幾何的理論研究最早可以追述到1792年🫲🏿🔭，當時數學界首屈一指的巨匠高斯就已經產生了非歐幾何思想的萌芽，到1817年已經達到了較為成熟的程度👩🏽‍🦲。他最初把這種新幾何稱為“反歐幾何”，最後改為“非歐幾何”💡。 非歐幾何在自然界中廣泛存在🍰，並在許多不同的研究領域發揮著重要作用🧑🏿，例如數學研究中的黎曼幾何👯🤌🏽、理論物理學中的Ads/CFT全息原理、以及愛因斯坦的廣義相對論等。最近，研究人員利用共面波導諧振器實驗實現了雙曲晶格對應的材料模型🦩🤾🏽。需要指出的是雙曲晶格是非歐幾裏得空間中一類非常重要的晶格模型🦮，其對應於常數負曲率空間中的正多邊形晶格平鋪結構🧑🏻‍🍳。該實驗極大推動了人們對於雙曲晶格不同物理特性的理論研究，包括雙曲能帶理論和雙曲晶體學等👵🏿。雙曲晶格與歐氏晶格最重要的區別是👨🏻‍🍳：雙曲晶格邊界格點的數目接近甚至大於體內格點的數目，並且這一關系在熱力學極限下仍然成立。另一方面，根據體邊界對應原理👐🦂，拓撲物態通常具有新奇的邊界響應。因此一個有趣的問題是🤜🏻：能否將雙曲晶格和拓撲物態獨特的邊界性質相結合，在雙曲空間中構造出不同於歐氏幾何拓撲態的雙曲拓撲態。如果雙曲拓撲態存在，在實驗上又該如何觀察這些新奇的拓撲物態？

研究亮點之一：邊界統治的雙曲反常量子霍爾效應及電路實現。

圖1. 邊界統治的雙曲反常量子霍爾效應👩🏼。

為了探究雙曲幾何和拓撲邊界態的相互作用💆🏼，研究人員首先將Haldane模型直接推廣到{6,4}雙曲晶格系統中👵，如圖1a-1c所示。簡單來講🚰，就是在{6,4}雙曲晶格的每一個六邊形結構中👈🏼，都引入實數最近鄰耦合和復數次近鄰耦合。新生成的模型被稱為雙曲Haldane模型。通過直接數值對角化的方法🧛，可以求得有限{6,4}雙曲Haldane模型的本征能譜和相應的本征態分布👩🏻‍🦯，如圖1d和1e所示🌷🤖。可以清晰的看到，能量為零附近的本征態為雙曲邊界態🧑🏻‍🎓。為了進一步證明雙曲邊界態的拓撲屬性，研究人員計算了實空間Chern數，如圖1f所示。可以看到雙曲邊界態能譜所對應的實空間Chern數具有非平庸的拓撲平臺，說明其具有類似於反常量子霍爾效應的拓撲屬性。而實空間Chern數沒有達到1是由於有限的格點數目導致的。進一步利用耦合模方程，研究人員研究了雙曲邊界態的單向拓撲傳輸特性🤲🏿，如圖1g所示。可以清晰的看到🧎，雙曲拓撲邊界態可以繞過缺陷單向傳輸。相比於歐氏空間的量子反常霍爾邊界態，雙曲拓撲邊界態具有顯著增強的邊界響應，即拓撲傳輸的通道(邊界點)數目大於或近似等於體內格點的數目。這一新奇的特性為設計高效的拓撲器件提供了新的途徑🗃🕺。

圖2. 基於雙曲電路網絡，實驗觀察雙曲反常量子霍爾效應😁。

基於凝聚態晶格模型與電子線路網路的一致性，研究人員設計並製備了雙曲電路(如圖2a所示)來觀察邊界統治的雙曲量子反常霍爾效應👨‍🦯‍➡️。圖2b和2c分別對應實驗測量和理論仿真的電路阻抗結果😒🗄。電路格點的阻抗響應對應於雙曲量子模型的局域態密度。可以看到，雙曲體點在紅色區域內沒有阻抗峰值，表明存在雙曲體帶帶隙。同時⬜️，雙曲電路的邊界格點在該帶隙中存在顯著的阻抗峰值◽️，表明拓撲邊界態的存在。圖2d展示的是邊界態所對應頻率下的電路阻抗分布圖。可以看出其與雙曲晶格模型中的拓撲邊緣態的概率幅分布完全一致。進一步☝️，研究人員通過測量電壓波包在雙曲電路網路中的時域特性，清晰地證明了邊界統治的雙曲邊界電壓傳輸👍，如圖2e-2j所示。

研究亮點之二：具有分形特點的高階雙曲零能角態及實驗觀測。

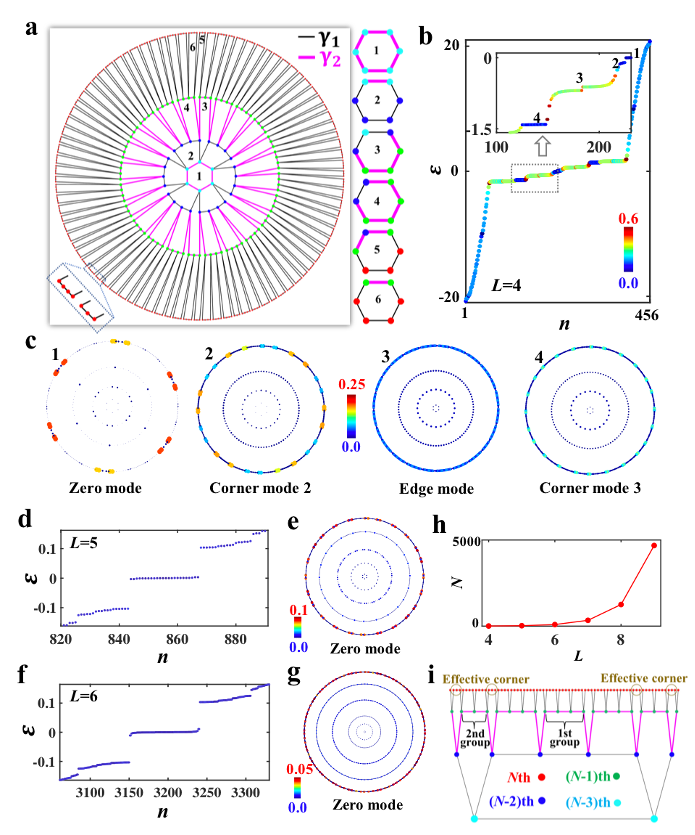
圖3. 具有分形特點的高階雙曲零能角態

除了一階雙曲量子反常霍爾邊界態🍸🤱，研究人員進一步研究了雙曲晶格中的高階零能角態。所設計的雙曲晶格模型顯示在圖3a中🌔，即在{6,4}雙曲晶格中引入二值化(黑線和粉線)的層內和層間最近鄰耦合🎱。當最外層的耦合強度對應於弱耦合時🤞🏼，高階角態就會產生。需要指出的是，不同於歐氏空間中0維角點的幾何特性，雙曲晶格的有效0維角點對應於具有不同耦合方式的最外層格點間的有效界面(如圖3i所示)𓀉。圖3b和3c展示了利用數值對角化方法計算的雙曲能譜和相應本征態的空間分布🙆🏽‍♀️。可以看到雙曲零能模的概率分布局域在最外層的0維格點上，展現了高階拓撲角態的特性。同時🧖🏼，除了零能模，在另外兩個能量附近也存在雙曲高階角態🈵。可以發現與歐氏空間的高階角態性質相似，雙曲高階角態也總是出現在雙曲邊界態的帶隙中🫃🏿。研究人員從三個方面進一步對高階零模的拓撲性質進行了證明🏋️‍♀️。首先🧘🏼‍♀️，通過改變二值化耦合強度的相對關系🎗，雙曲能譜發生了帶隙閉合再打開的過程。同時🛤，該過程伴隨著雙曲高階零能模從無到有的變化過程🏙，是拓撲相變的重要特征。其次，雙曲高階拓撲態具有與C6-高階拓撲絕緣體相同的拓撲相變特點。最後，通過引入無序可以發現雙曲高階零能角態具有很強的魯棒性🍫，這與雙曲晶格中由幹涉引起的局域化效應顯著不同。另外研究人員計算了不同尺寸下的雙曲能譜和本征態的分布👎🏿，如圖3d-3g所示🧝🏿‍♂️🙅🏻。圖3h給出了雙曲零能模的數量與雙曲晶格尺寸的關系🧖🏽‍♂️。可以看到通過增大雙曲晶格的尺寸，雙曲零能模式的數量也急劇增加👭。該現象與分形幾何結構中的高階拓撲角態相似。需要強調的是，這一新奇的現象是源於雙曲晶格獨特的邊界響應👵🏼，即邊界格點的數目隨雙曲晶格層數的增加而呈現指數增長的趨勢，使得邊界有效0維角點也具有指數增長的特點。

為了在實驗上觀察雙曲高階零能角態👨🏻‍🔬🤖，研究人員設計並製備了相應的雙曲電路網絡📱，如圖4a所示。圖4b和4c分別對應實驗測量和理論仿真的電路阻抗結果。可以看到雙曲晶格的邊界點在藍色區域所對應的頻率範圍內有顯著的阻抗峰值⛩，而體點在相應頻率範圍沒有阻抗響應，表明雙曲邊界態存在於雙曲體態的帶隙中🈵。同時雙曲晶格的角點在紅色區域內有顯著的阻抗峰值，而邊界格點在該頻率範圍沒有阻抗峰值。這一現象表明雙曲高階角態存在於雙曲邊界態的帶隙中。為了進一步展現不同雙曲高階角態的空間分布，研究人員對電路的導納矩陣進行了重構🪰🧙🏿，並利用重構的導納矩陣得到了不同雙曲高階角態的空間分布圖，如圖4d所示🦸‍♀️。可以看出測得的高階角態分布與雙曲晶格模型的結果完全一致👩🏻‍🎤。

圖4. 基於雙曲電路網絡👏，實驗觀察高階雙曲零能模。

論文鏈接🙎‍♂️🦸🏻‍♀️：https://www.nature.com/articles/s41467-022-30631-x